This document is a seminar note on singular homology.

Before reading this article, make sure you have known the Chapter 1-3 of An Introduction to Algebraic Topology, written by Rotman.

You can download the pdf version from this link.

Reference

• An Introduction to Algebraic Topology, Rotman
• Topology and Geometry, Bredon
• 代数学方法 卷一：基础架构, 李文威
• nlab

Why should we learn homology?

When we use calculus to solve physical problems, we often encounter functions like

where $k,Q$ are constants.

It can be noticed that $(0,0,0)$ is a singularity of it, and when integrating this function, we always choose an integration path or integration surface that bypasses the singularity. Moreover, from Maxwell's equations (or Stokes' theorem), we know that if we choose a closed surface in space for integration, the value of the integration only relates to the singularities inside. Here, the singularities can be considered as holes in the space defined by the function. This is why we are interested in the holes in space and consequently study their properties.

Homology was initially defined as closed curves or surfaces with the same integral values, but this definition cannot adapt to general topological spaces. From a geometric intuition, a hole should be a type of topological invariant that remains unchanged under homeomorphism. Therefore, we need to find some new methods to define homology, and thereby study the properties of these holes. Next, we will begin to learn a definition method of homology, which is the singular homology.

1. Definition of Singular Homology

Let's begin with some basic definitions.

1.1 Definition.

Let $A$ be a set and $F=\{f:A\to \mathbb Z;f^{-1}(\mathbb Z-\{0\}) \text{ is finite}\}$.

We can define a binary operation

It's easy to check that $(F,+)$ is an abelian group. And we call it the free abelian group on $A$​​.

We usually denote $f\in F$ as $\sum_{a\in A} f(a)a$.

For example, we can use $2a_1-a_2$ to denote $f:A\to \mathbb Z,a\mapsto\begin{cases}2,&a=a_1,\\-1,&a=a_2,\\0,&a\ne a_1,a_2.\end{cases}$

We also use $\mathbb Z^{\oplus A}$ to denote the free abelian group on $A$.

The free abelian group has a universal property.

1.2 Theorem (Universal Property).

Let $A$ be a set and $F$ be the free abelian group on it.

$G$ is an abelian group and there is a function $f:A\to G$. Then there exists a unique group homomorphism $\sigma:F\to G$ making diagram

commute, where $i$​ is the inclusion. And $\sigma$ is called extending by linearity.

Proof.

Define $\sigma:F\to G,\sum_i c_ia_i\mapsto \sum_i c_if(a_i)$. It's easy to check that $\sigma$​ is a group homomorphism.

Then let's prove $\sigma$ is unique.

Let $\sigma_0$ is another function fit the theorem. Then we have

Therefore, $\sigma_0=\sigma$ and $\sigma$ is unique. $\square$​

1.3 Definition.

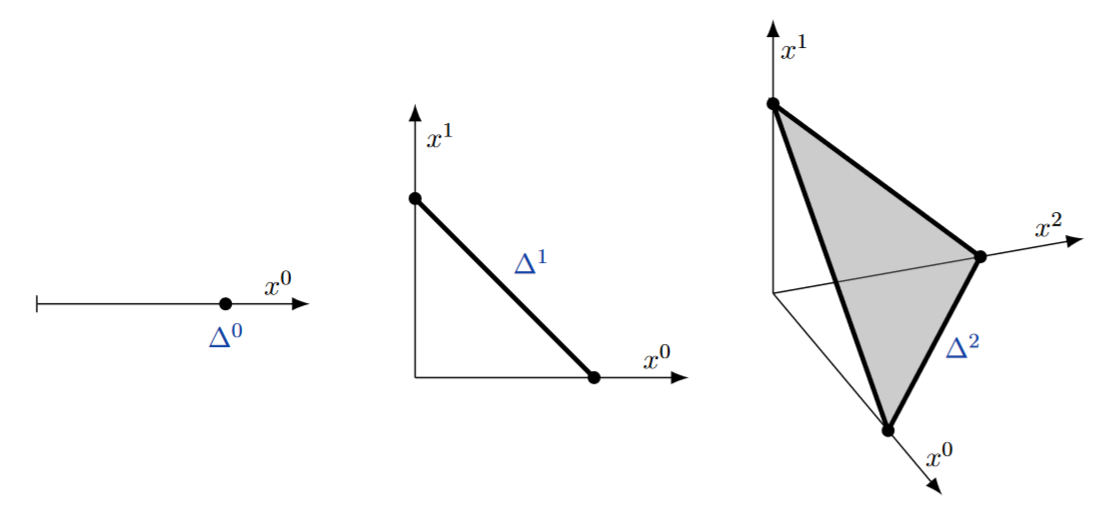
For $n\in \mathbb N$, the standard $n$​-simplex is

We can see their graphs in this picture:

We can denote $\Delta^n$ as $[e_0,e_1,\dots,e_n]$, where $e_0,e_1,\dots,e_n$ are vertices of $\Delta^n$​.

Sometimes, we will see $\Delta^1$ as $I$ with $(1-t,t)\mapsto t$.

When we perform integrations on some geometric shapes, these shapes often have an orientation. Similarly, we can also define an orientation for simplices.

1.4 Definition.

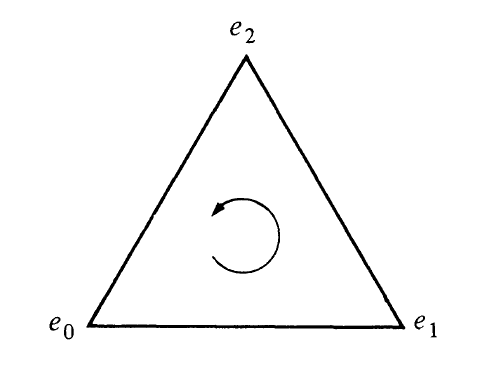
An orientation of $\Delta^n=[e_0,e_1,\dots,e_n]$ is a linear ordering of its vertices.

An orientation thus gives a tour of the vertices. For example, the orientation $e_0<e_1<e_2$ of $\Delta^2$ gives a counterclockwise tour.

Two orientations of $\Delta^n$ are the same if, as permutations of $\{e_0,e_1,\dots,e_n\}$, they have the same parity (i.e., both are even or both are odd); otherwise the orientations are opposite.

1.5 Definition.

Let $X$ be a topological space, $n\ge 0$. A (singular) $n$-simplex in $X$ is a continuous function $f:\Delta^n\to X$.

$S_n(X)$ denotes the free abelian group generated by all singular $n$-simplices in $X$​; and we define $S_m(X)=0$ for all integers $m<0$.

And we call an element in $S_n(X)$ is an $n$-chain on $X$.

Let's consider what the elements in $S_n(X)$ are.

Let $\sum_i m_i\sigma_i$ be an $n$-chain, where $m_i\in \mathbb Z$ and $\sigma_i:\Delta^n\to X$ is continuous. We can regard $\sigma_i$ as a $n$-dimensional geometric shape on $X$ (this may not be accurate), and the sign of $m_i$ denote the orientation of $\gamma_i$. Then we can consider $\sum_i m_i\sigma_i$ as a combination of some $n$-dimensional geometric shapes on $X$.

How to use $n$-chains to describe holes in $X$?

When X is a plane with some holes, we can notice that the holes in the plane can be surrounded by a 1-chain, whose simplices precisely form some "closed curves".

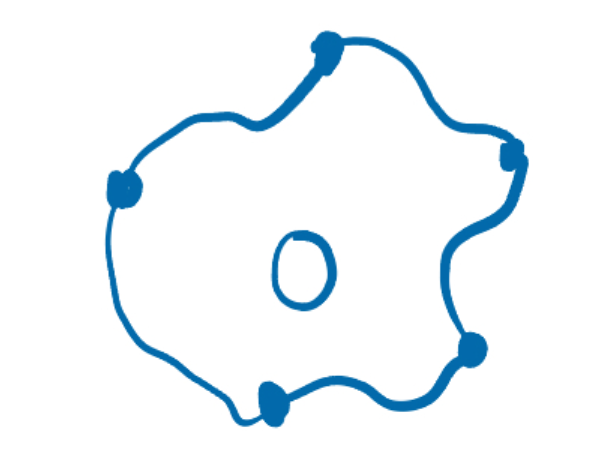
Therefore, we need a method to find "closed curves" and try to use them to describe holes.

As we can see, "closed curves" have no boundary while "open curves" always have at least two points as its boundary.

Thus, we need to describe the boundary of an $n$​-chain.

1.6 Definition.

Define the $i$-th face map of $\Delta^n$

We can consider that the usage of these maps is to take out the face opposite to the $i$-th vertex in the n-simplex. With these maps, we can define the boundary of $n$-chains.

1.7 Definition.

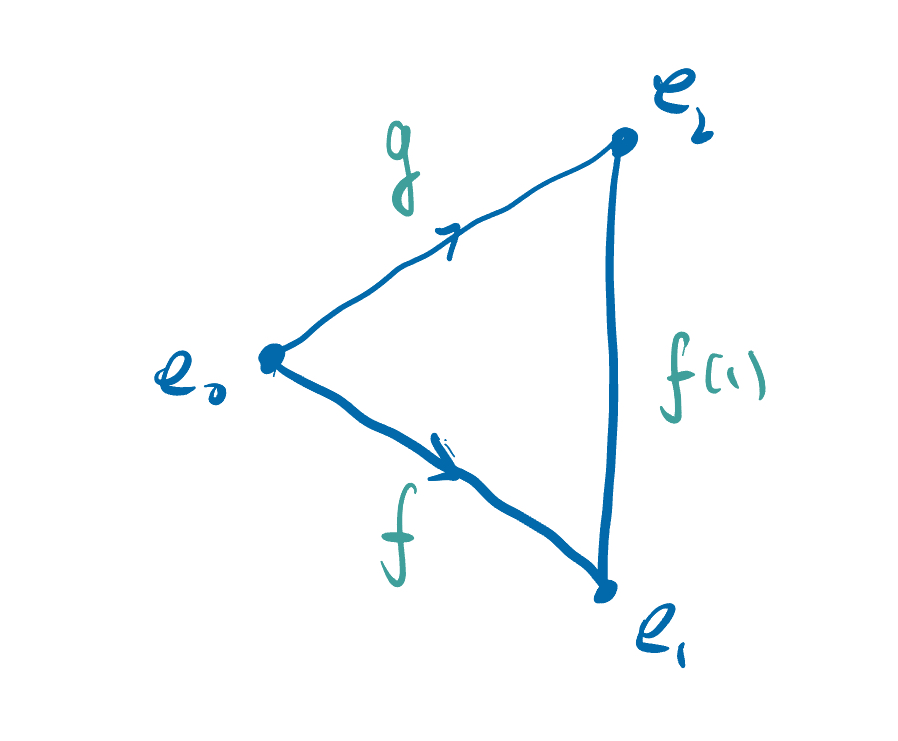
If $\sigma:\Delta^n\to X$ is continuous and $n>0$, then its boundary is

if $n=0$, define $\partial_0\sigma=0$​​.

As shown in the following figure, defining the boundary in this way is consistent with our geometric intuition.

Then we extend $\partial_n$ by linearity, and hence we get a group homomorphism $\partial_n:S_n(X)\to S_{n-1}(X)$, for all $n\in \mathbb N$. The homomorphisms $\partial_n$​ are called boundary operators.

Strictly speaking, we ought to write $\partial_n^X$ instead of $\partial_n$ since these homomorphisms do depend on $X$​​; however, this is rarely done.

For each $X$, we have constructed a sequence of free abelia groups and homomorphisms

, called the singular complex of $X$; it is denoted by $(S_*(X),\partial)$ or, more simply, by $S_*(X)$.

Then, we can find all "closed curves".

1.8 Definition.

The group of (singular) $n$-cycles in $X$, denoted by $Z_n(X)$, is $\ker \partial_n$.

Although we can find all "closed curves" in a plane $X$, we still can't describe holes in $X$. We can note that the holes in the plane can be surrounded by 1-chains, but cannot be covered by 2-chains.

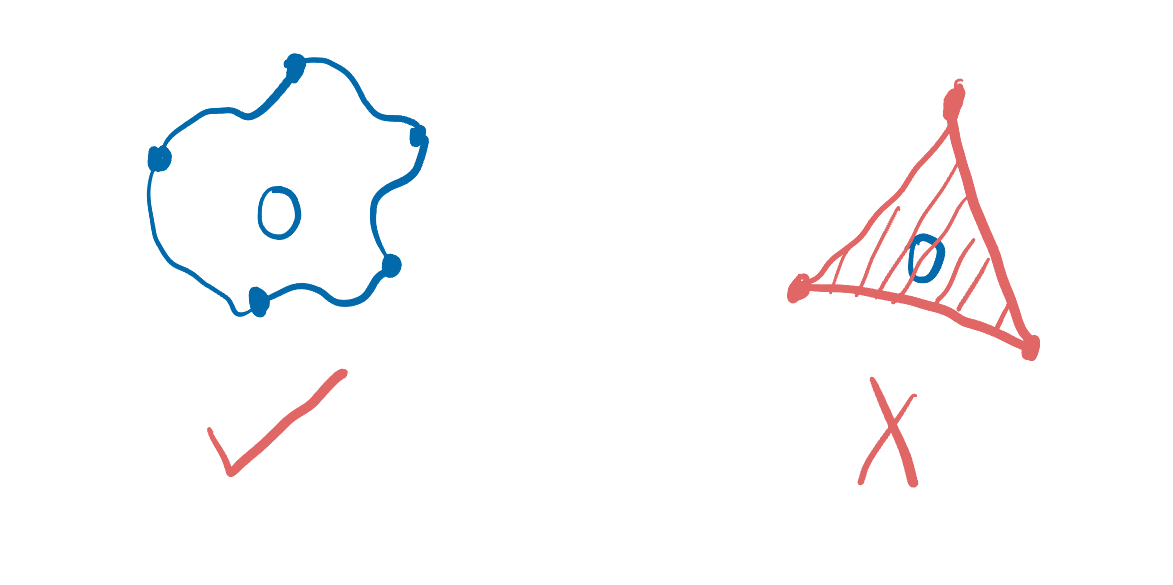
Therefore, we know that there are some "closed curves", boundaries of $2$-chains, surrounding no holes!

1.9 Definition.

The group of (singular) $n$-boundaries in $X$, denoted by $B_n(X)$, is $\operatorname{im} \partial_{n+1}$.

Wait, are $n$-boundaries really $n$-cycles?

1.10 Lemma.

If $j<i$, the face maps satisfy

It's easy to prove by using the definition of $\varepsilon_i^n$.

1.11 Theorem.

For all $n$, we have $\partial_n\partial_{n+1}=0$; and thus $B_n(X)\subset Z_n(X)$.

Proof.

Since $S_{n+1}(X)$ is generated by all $(n+1)$-simplices $\sigma$, it suffices to show that $\partial\partial\sigma=0$ for each such $\sigma$.

Eventually, we can describe holes by using the quotient group.

1.12 Definition.

For each $n$, the $n$-th (singular) homology group of a space $X$ is

The coset $z_n+B_n(X)$, where $z_n$ is an $n$-cycle, is called the homology class of $z_n$, and it is denoted by $\operatorname{cls} z_n$.

2. Functorialities of $S_*$ and $H_n$

When we view $S_*$ and $H_n$​ from the perspective of category theory, we can find that they are actually functors.

2.1 Definition.

A (chain) complex is a sequence of abelian groups and homomorphisms

, where $n\in \mathbb Z$, such that $\partial_n\partial_{n+1}=0$ for each $n\in \mathbb Z$. The homomorphism $\partial_n$ is called the differentiation of degree $n$, and $C_n$ is called the term of degree $n$.

The complex above is denoted by $(C_*,\partial)$ or, more simply, by $C_*$.

2.2 Definition.

If $(C_*,\partial)$ and $(C'_*,\partial')$ are complexes, a chain map $f:(C_*,\partial)\to(C_*',\partial')$ is a sequence of homomorphisms $\{f_n:C_n\to C_n'\}$ such that the diagram

commutes.

2.3 Theorem.

All complexes and chain maps form a category, denoted by $\mathbf{Comp}$, when one defines composition of chain maps coordinatewise: $\{g_n\}\circ\{f_n\}:=\{g_n\circ f_n\}$.

It's easy to prove this is a category.

2.4 Theorem.

Let $f:X\to Y$ be a continuous function and $\sum_im_i\sigma_i\in S_n(X)$, where $m_i\in \mathbb Z$ and $\sigma_i$ is an $n$-simplex for all $i$. Define $f_\#(\sum_im_i\sigma_i)=\sum_i m_if\circ\sigma_i\in S_n(Y)$, and then we get a sequence of homomorphisms $\{f_\#:S_n(X)\to S_n(Y)\}$. (Note: $f_\#$ does depend on $n$, but we usually don't give it a subscript.)

Define $S_*(f):=f_\#$. And then $S_n:\mathbf{Top}\to \mathbf{Ab},S_*:\mathbf{Top}\to \mathbf{Comp}$ are functors.

Proof.

Let $f:X\to Y$ and $g:Y\to Z$ are continuous functions. Then, for any $n$-simplex $\sigma$ in $X$, we have

By the universal property of free abelian groups, we have $(f\circ g)_\#=f_\#\circ g_\#$.

Let $1_X$ be the identity map of $X$. Then, for any $n$-simplex $\sigma$ in $X$, we have

Similarly, because of the universal property of free abelian groups, we have $(1_X)_\#=1_{S_n(X)}$​.

Consequently, $S_n$ is a functor.

Next, to check $S_*$ is a functor, we need to verity the commutation of diagram

; for any $n$-simplices $\sigma$ in $X$​, we have

2.5 Definition.

Let $(C_*,\partial)$ be a chain complex. Then, there are

Similarly, $Z_n(C_*)$ is called the group of $n$-cycles, $B_n(C_*)$ is called the group of $n$-boundaries, and $H_n(C_*)$ is called $n$-th homology group.

Let $f:(C_*,\partial)\to (C_*'.\partial')$ be a chain map. Define

We also denote $H_n(f)$ as $f_*$. If $g:X\to Y$ is continuous. We denote $H_n(S_*(g))$ as $g_*$, too.

2.6 Theorem.

$H_n:\mathbf{Comp}\to \mathbf{Ab}$ is a functor.

And thus, the composition $H_n\circ S_*:\mathbf{Top}\to \mathbf{Ab}$ is also a functor. We always write $H_n\circ S_*$ as $H_n$.

Proof.

Let $C_*,C_*',C_*''$ be chain complexes, and $\{f_n\}:C_*\to C_*',\{g_n\}:C_*’\to C_*''$ be chain maps.

Then we have

and

Therefore, $H_n$ is a functor. $\square$

2.7 Lemma.

Let $A$ be a subspace of $X$ with inclusion $j:A\hookrightarrow X$. Then $j_\#:S_n(A)\to S_n(X)$ is an injection for every $n\ge 0$.

Proof.

Let $\gamma = \sum m_i\sigma_i\in \operatorname{ker} j_\#$, where $\sigma_i$ are distinct $n$-simplices.

Then we have $j_\#(\gamma)=\sum m_i (j\sigma_i)=0$.

Since $j\sigma_i=j\sigma_{i'}\Rightarrow \sigma_i=\sigma_{i'}$, we have $j\sigma_i$ are distinct. Therefore, for each $i$, $m_i=0$. $\square$

Recall: Coproduct

Let $\mathscr C$ be a category, $\{X_\lambda;\lambda\in \Lambda\}\subset \operatorname{Obj}(\mathscr C)$ is a set of some objects.

Then the coproduct is an object $\coprod_\lambda X_\lambda$ with inclusions $i_\lambda:X_\lambda\to \coprod_\lambda X_\lambda$ such that for all morphisms $\{f_\lambda:X_\lambda\to L\}$, there is a unique morphism $\alpha$ make all diagrams like

commute.

Coproduct is a specific example of colimits (direct limits). Next, I will show you that $H_n$​ preserve coproduct. Actually, $H_n$ is co-continuous; that is $H_n$ preserve colimits.

2.8 Lemma.

Functor $S_*$ preserve coproduct; that is $\{X_\lambda;\lambda\in \Lambda\}$ is a set of topological spaces and let $X=\coprod X_\lambda$, and then we have $S_*(X)\cong \coprod S_*(X_\lambda)$.

Proof.

Let $j_\lambda:X_\lambda\to X$ be inclusions.

It's sufficient to prove $S_*(X)$ has the same universal property as $S_*(\coprod X_\lambda)$; that is, for all complexes $L_*$ and chain maps $f_\lambda:S_*(X_\lambda)\to L_*$, there is a unique chain map $\varphi$ such that the diagrams

commute.

• Existence of $\varphi$:

  For each $n$-simplex $\sigma$, since $\Delta^n$ is path connected, there is a $\lambda\in \Lambda$ such that $\operatorname{im}\sigma\subset j_\lambda(X_\lambda)$.

  Therefore, for each $\gamma=\sum m_i \sigma_i\in S_n(X)$ with $\sigma_i$ are $n$-simplices, we have $\gamma=\sum_i m_ij_{\lambda_i\#}j_{\lambda_i\#}^{-1}(\sigma_i)$, where $\sigma_i\subset j_{\lambda_i}(X_{\lambda_i})$.

  Define

  It's easy to know $\varphi_n$ are group homomorphisms. We should show that $\varphi=\{\varphi_n\}$​ is a chain map.

  For $f_\lambda$ and $j_{\lambda\#}$ are chain maps, we have commutative diagrams

  and

  ; hence

• Uniqueness of $\varphi$:

  If there are $\varphi$ and $\psi$ both satisfy the properties, then we have

  Therefore, $\varphi = \psi$. $\square$

2.9 Theorem.

Functor $H_n$ preserve coproduct; that is $\{C_{\lambda*}\}$ is a set of chain complexes, and then we have $H_n(\coprod_\lambda C_{\lambda*})\cong\coprod_\lambda H_n(C_{\lambda*})$.

Proof.

Let $C_*=\coprod_\lambda C_{\lambda*}$ and $j_\lambda:C_{\lambda*}\to C_*$ be inclusions.

It's sufficient to prove $H_n(C_*)$ has the same universal property as $\coprod_\lambda H_n(C_{\lambda*})$; that is, for all abelian groups $L$ and homomorphisms $f_\lambda :H_n(C_{\lambda*})\to L$, there is a unique homomorphism $\varphi:H_n(C_*)\to L$, such that the diagrams

commute.

• Existence of $\varphi$:

Each $\operatorname{cls} z\in H_n(C_*)$, where $z\in Z_n(C_*)$, can be write as $z=\sum z_\lambda$ with $z_\lambda\in j_\lambda(C_{\lambda,n})$​.

Define

Next, let's show that $\varphi$ is well-defined.

Let $b\in B_n(C_*)$, and then there is $\gamma\in C_{n+1}$ with $\partial \gamma=b$​.

Because of the commutative diagram

, we have

Thus, $\sum j_\lambda(b_\lambda-\partial\gamma_\lambda)=0$​.

Consequently, we have $b_\lambda=\partial\gamma_\lambda$; hence $\varphi(\operatorname{cls} b)=\sum f_\lambda(\operatorname{cls}b_\lambda)=0$.

• Uniqueness of $\varphi$:

If there are $\varphi$ and $\psi$ both satisfy the properties, then we have

Therefore, $\varphi = \psi$. $\square$

2.10 Corollary.

If $\{X_\lambda;\lambda\in \Lambda\}$ is the set of path components of $X$, then we have

3. Dimension Axiom and Homotopy Axiom

In this section, we will introduce two axioms of homoblogy theory.

3.1 Theorem (Dimension Axiom).

If $X$ is a one-point space, then $H_n(X)=0$ for all $n\ge 1$.

Proof.

For each $n\ge 0$, there is only one singular $n$-simplex $\sigma_n:\Delta^n\to X$, where $\sigma_n$ is a constant map.

Therefore, $S_n(X)=\left<\sigma_n\right>$. Then, let's compute the boundary operators:

It follows that, for all $n\ge 1$,

Thus, for each $n\ge 1$,we have two conditions:

• If $n$ is odd, we have $Z_n(X)=H_n(X)$ and $\sigma_n \in B_n(X)$. Hence, $Z_n(X)=B_n(X)$.
• If $n$ is even, we have $Z_n(X)=0$.

Therefore, $H_n(X)=0$. $\square$

3.2 Definition.

A space $X$ is called acyclic if $H_n(X)=0$ for all $n\ge 1$.

3.3 Proposition.

• If $X=\emptyset$, then $H_n(X)=0$ for all $n\ge 0$.
• If $X$ is a one-point space, then $H_0(X)= \mathbb Z$​​.
• If $X$ is the Cantor set, then $H_n(X)=\begin{cases}\mathbb Z^{\oplus X},&n=0,\\0,&\text{otherwise}.\end{cases}$

3.4 Theorem.

If $X$ is a non-empty path-connected space, then $H_0(X)=\mathbb Z$.

Hence, for any topological space $Y$, $H_0(Y)=\coprod_{\lambda\in\Lambda} H_0(Y_\lambda)=\mathbb Z^{\oplus\Lambda}$, where $\{Y_\lambda;\lambda\in \Lambda\}$ are path components of $Y$.

Proof.

For $\partial_0=0$, we have $Z_0(X)=S_0(X)$.

(We will use $x\in X$ to denote the map $\Delta^0\to X,e_0\mapsto x$.)

Define $B=\{\sum_{i=1}^t m_i x_i;\sum m_i=0\}$. It's obvious that $B$ is a subgroup of $S_0(X)$.

Next, let's prove $B=B_0(X)$.

• If $\sum m_i x_i\in B_0(X)$, then there is $\gamma=\sum a_i\sigma_i\in S_1(X)$ with $\partial\gamma=\sum m_i x_i$.

  And then, we have $\partial\gamma=\sum (a_i\sigma_i\varepsilon_0-a_i\sigma_i\varepsilon_1)=\sum m_i x_i$.

  Since $x_i,\sigma_i\varepsilon_0,\sigma_i\varepsilon_1$ are generators, $\sum m_i=\sum (a_i-a_i)=0$.

  Therefore, $\sum m_i x_i\in B$.

• Let $\sum m_i x_i\in B$, and fix a point $x_0\in X$.

  Let $L_x:\Delta^1\to X$ be a path from $x_0$ to $x$ (consider $\Delta^1$ as $I$).

  Then let $\gamma=\sum m_iL_{x_i}\in S_1(X)$. We can find that

  Therefore, $\sum m_ix_i\in B_0(X)$.

Define $\varphi:Z_0(X)\to \mathbb Z,\sum m_ix_i\to \sum m_i$. It's trivial that $\varphi$ is a homomorphism with $\ker \varphi=B$.

Consequently, $H_0(X)=Z_0(X)/B_0(X)\cong \mathbb Z$. $\square$

Next, we will learn the homotopy axiom; that is if $f,g$ are two homotopic continuous maps, then we have $f_*=g_*$. However, we will not prove this theorem directly. Let us prove it step by step.

3.5 Lemma.

If $X$ be a bounded convex subset of $\mathbb R^k$, then $H_n(X)=0$ for all $n\ge 1$.

Proof.

Fix a point $b\in X$. Let $\sigma$ be a $n$-simplex.

For all $n\ge 0$, define

And then define

It's easy to check $c_n$​ is a homomorphism.

When $n\ge 1$, we claim that, for a $n$-chain $\gamma$,

If $(*)$ is true, we have, for all $z\in Z_n(X)$,​

Consequently, $z\in B_n(X)$; hence, the lemma has been proved.

Next, we will prove $(*)$.

Let $\sigma$ be a $n$-simplex. And then we have

; and

Thus, we have $\partial c_n\sigma=\sigma-c_{n-1}\partial\sigma$.

By using the universal property of free abelian groups, we proved $(*)$. $\square$​

3.6 Definition.

Let $C_*,C_*'$ be two chain complexes, and $f$ and $g$​ be chain maps. We call $f$ and $g$ are (chain) homotopic if there are homomorphisms $P_n:C_n\to C_{n+1}'$ such that $\partial P_{n}+P_{n-1}\partial=f_n-g_n$​​ for each $n$.

The following diagram is NOT commutative.

3.7 Theorem.

If $f$ and $g$ are chain homotopic, then we have $H_n(f)=H_n(g)$ for each $n$.

Proof.

Let $\operatorname{cls} z\in H_n(C_*)$, and then we have

3.8 Lemma.

Let $X$ be a space and, for $i=0,1$, define

Let $f,g:X\to Y$ be two homotopic continuous maps.

If $H_n(\lambda_0^X)=H_n(\lambda_1^X)$, then we have $H_n(f)=H_n(g)$.

Proof.

Let $F:f\simeq g$ be the homotopy. Then we have

3.9 Definition.

Let $\mathscr C,\mathscr D$ be two categories, and $F,G:\mathscr C\to \mathscr D$ be two (covariant) functors. A natural transformation $\theta:F\to G$ is a collection of morphisms $\{\theta_X:F(X)\to G(X);$$X\in\operatorname{Obj}(\mathscr C)\}$​ such that the diagrams

commute.

3.10 Theorem (Homotopy Axiom).

If $f,g:X\to Y$ be two homotopic continuous maps, then

Notations:

Let $f:A\to B,g:C\to D$ are maps. Define

Let $h:A\to E$ is a map. Define

Proof.

As what we discussed above (3.5, 3.6 and 3.7), it's sufficient to prove $\lambda_{0\#}^X$ and $\lambda_{1\#}^X$ are chain homotopic.

Define $T_n(X)=S_{n+1}(X\times I)$, and $T_*(f)=(f\times 1_I)_\#$, where $f$ is a continuous map.

It's easy to check $T_n:\mathbf{Top}\to \mathbf{Ab}$ is a functor.

Actually, we will construct natural transformations $P_n=\{P^X_n:S_n(X)\to T_n(X)\}$ such that

Since $P_n$ is a natural transformation, we also have a commutative diagram

. Let $\delta:\Delta^n\to \Delta^n$ be the identity map and $\sigma$ be a $n$-simplex on $X$. (We will use $\Delta$ in short for $\Delta^n$ in the remaining part of this proof.)

If $P$ exists, we can notice that

Therefore, in order to construct $P_n^X(\sigma)$, we only need to construct $P_n^\Delta(\delta)$.

Next, let's construct $P$ by induction on $n$.

• Base step for induction ($n=0$​):

  We have $P_{-1}^X=0$ for $0\to S_0(X\times I)$ only has one homomorphism.

  Let $\delta:\Delta^0\to \Delta^0$​ be the identity map.

  Define

  and, for $0$-simplex $\sigma$,

  By extending $P_0^X$ by linearity, we get homomorphisms $P_0^X:S_0(X)\to S_1(X\times I)$.

  Then we should verify the inductive hypothesis.

  • For $0$-simplex $\sigma$, we have

    Consequently,

    And by the universal property of the abelian groups, we know $(*)$ is true.

  • (Naturality of $P_n$​)

    Let $f:X\to Y$ be a continuous map. Then we have

    Similarly, by the universal property, we know $P_0$ is a natural transformation.

• Assume that $n>0$​​.

  Let $\delta:\Delta^n\to\Delta^n$​ be the identity map.

  If $(*)$ is true, we have

  Therefore, we need to prove $(\lambda_{0\#}^\Delta-\lambda_{1\#}^\Delta-P_{n-1}^\Delta\partial)(\delta)\in B_n(\Delta^n\times I)$.

  Since $\Delta^n\times I$ is a bounded convex subset of $\mathbb R^{n+2}$, by lemma 3.4, we have $H_n(\Delta^n\times I)=0$; that is $B_n(\Delta^n\times I)=Z_n(\Delta^n\times I)$.

  Consequently, we only need to prove $(\lambda_{0\#}^\Delta-\lambda_{1\#}^\Delta-P_{n-1}^\Delta\partial)(\delta)\in Z_n(\Delta^n\times I)$.

  Since

  we have $(\lambda_{0\#}^\Delta-\lambda_{1\#}^\Delta-P_{n-1}^\Delta\partial)(\delta)\in B_n(\Delta^n\times I)$; that is $\exists \beta_{n+1}\in S_{n+1}(\Delta\times I)$, such that $\partial\beta_{n+1}=(\lambda_{0\#}^\Delta-\lambda_{1\#}^\Delta-P_{n-1}^\Delta\partial)(\delta)$.

  Define

  and

  By extending $P_n^X$ by linearity, we get homomorphisms $P_n^X:S_n(X)\to S_{n+1}(X\times I)$.

  Next, we need to verify inductive hypothesis.

  • For $n$-simplex $\sigma$​, we have

    And by the universal property of the abelian groups, we know $(*)$ is true.

  • (Naturality of $P_n$)

    Let $f:X\to Y$ be a continuous map. Then we have

    Similarly, by the universal property, we know $P_n$ is a natural transformation. $\square$

Therefore, we can also see $H_1$ as a functor from $\mathbf{hTop}$ to $\mathbf{Ab}$.

3.11 Corollary.

If $X$ and $Y$ have the same homotopic type, then we have $H_n(X)\cong H_n(Y)$.

3.12 Corollary.

If $X$ is contractible, then $H_n(X)=0$ for all $n>0$, and $H_0(X)=\mathbb Z$.

4. Hurewicz Theorem

In this section, let's talk about the relationship between $\pi_1$ and $H_1$. Additionally, all the topological spaces in this section are path-connected, and we always choose a base point $x_0\in X$.

We will denote the abelianized fundamental group of $X$ at $x_0$ as $\tilde\pi_1$; that is $\tilde \pi_1=\pi_1(X,x_0)/\pi_1'(X,x_0)$, where $\pi_1'(X,x_0)$ is the commutator subgroup of $\pi_1(X,x_0)$.

We will use $[f]$ stands for a homotopy class; $\overline f$ stands for the coset of $[f]$ in $\tilde\pi_1$; and $f\simeq g$ stands for "$f$ is homotopic to $g$", while "$f\sim g$ stands for $f$ is homologous to $g$​".

4.1 Lemma.

If $f$ and $g$ are paths in $X$ such that $f(1)=g(0)$ then the $1$-chain $f*g-f-g$ is a boundary.

Proof.

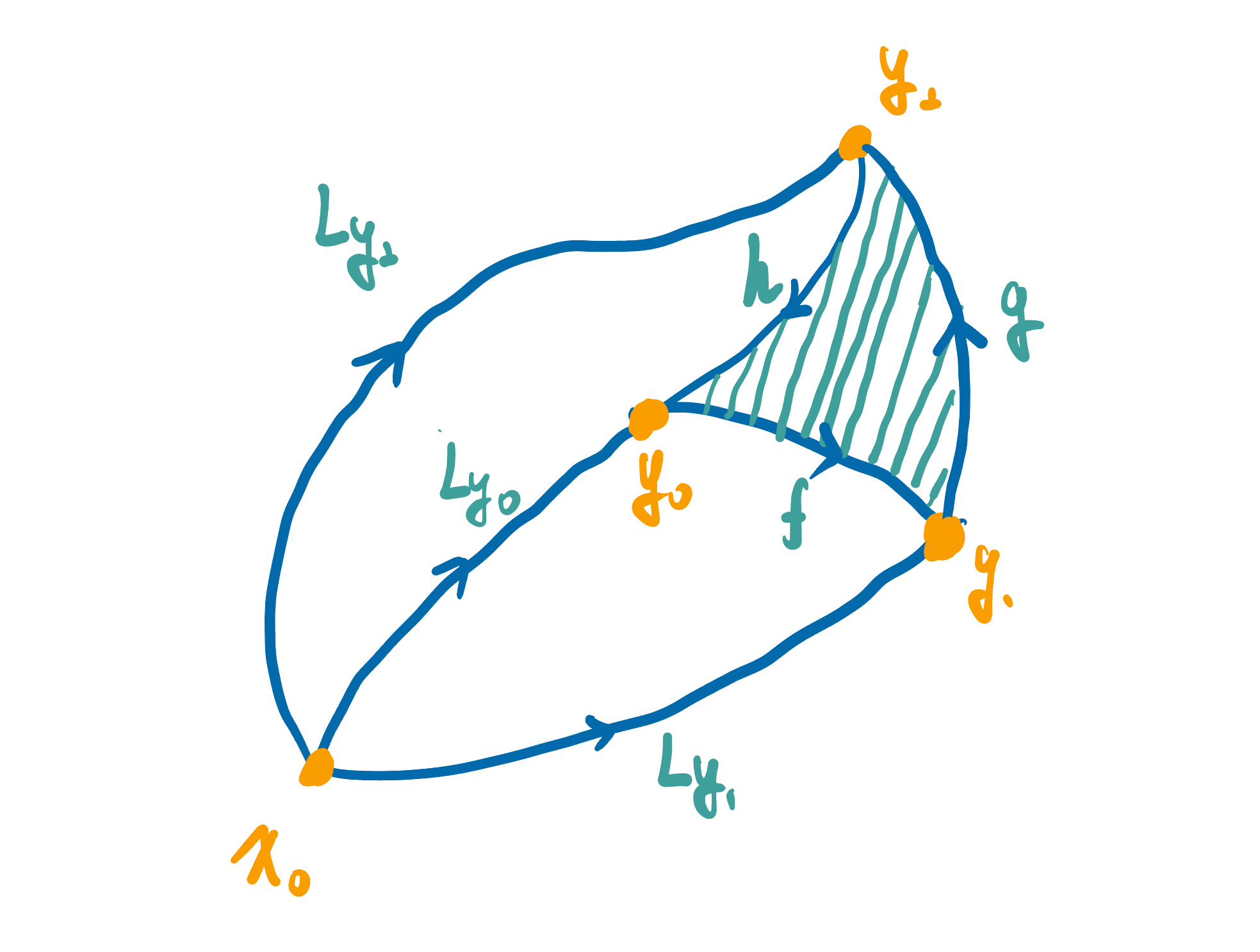
Define a continuous map $\sigma:\Delta^2\to X$​ as indicated by the following picture.

In more detail, first define $\sigma$ on $\Delta^2$:

Now define $\sigma$ on all of $\Delta^2$ by setting it constant on the line segment with endpoints $a=a(t)=(1-t,t,0)$ and $b=b(t)=((2-t)/2,0,t/2)$, and constant on the line segments with endpoints $c=c(t)=(0,1-t,t)$ and $d=d(t)=((1-t)/2,0,(1+t)/2)$.

Then we can find that $\partial\sigma=f+g-f*g$. $\square$

4.2 Lemma.

If $f$ is a constant, then $f$ is a boundary.

Proof.

By lemma 3.1, we have $f*f-f-f=-f$ is a boundary. $\square$

4.3 Lemma.

If $f$ and $g$ are paths with $f\simeq g\text{ rel }\dot{I}$, then $f\sim g$​​.

And thus $f*f^{-1}$ is a boundary; hence, $f+f^{-1}$ is a boundary by lemma 3.2.

Proof.

Let $F:f\simeq g\text{ rel }\dot{I}$ be the homotopy.

Define

The definition of this map is illustrated in the following picture.

Then, it's obvious that $\partial\sigma=f-g+c$, where $c:(t_0,t_1)\mapsto f(1)$ is a constant map.

Therefore, by lemma 3.2, $f-g\in B_1(X)$. $\square$

4.4 Definition.

The Hurewicz map is

By lemma 4.1, 4.2 and 4.3, we can know that $\phi$ is a well-defined homomorphism.

As we can see, $H_1(X)$ is a abelian group, while $\pi_1$ may not. Therefore, $\phi$ induces a homomorphism

In fact, $\phi_*$​ is an isomorphism, I will show you soon.

To prove $\phi_*$​ is an isomorphism, we can try to construct its inverse.

Since $X$ is path-connected, for all $x\in X$ there is a path $L_x$ from $x_0$ to $x$​.

For each $1$-simplex $\sigma$, which is also a path, define $\psi(\sigma)=\overline{L_{\sigma(e_0)}*\sigma*L^{-1}_{\sigma(e_1)}}$​​.

Then by extending $\psi$ by linearity, we get a homomorphism $\psi:S_1(X)\to \tilde \pi_1(X,x_0)$.

To ensure $\psi$ can induce a map from $H_1(X)$ to $\tilde\pi_1$, we should check $B_0(X)\subset\ker\psi$.

4.5 Lemma.

The map $\psi$ takes the group $B_1(X)$ into $1\in\tilde\pi_1$.

Proof.

Let $\sigma$ be a $2$-simplex. Let $\sigma(e_i)=y_i$ for $i=1,2,3$ and $f=\sigma\varepsilon_2,g=\sigma\varepsilon_0,h=(\sigma\varepsilon_1)^{-1}$​.

Then

For $f*g*h$ is a boundary of $2$-simplex, which is nullhomotopic rel $\dot I$ (Rotman, Exercise 3.4), $\psi(\partial\sigma)=1$.

Therefore, by the universal property of the abelian group, we get $B_0(X)\subset\ker\psi$. $\square$

Consequently, $\psi$ induces the homomorphism $\psi_*:H_1(X)\to \tilde\pi_1$.

If $f$ is a loop, then we can easily find $\psi_*\phi_*(\overline f)=\psi_*\operatorname{cls} f=\overline{L_{x_0}fL_{x_0}^{-1}}=\overline f$.

Thus, to show $\psi_*$ is the inverse of $\phi_*$, it's sufficient to prove $\phi_*\psi_*=1$.

4.6 Lemma.

If $\gamma$ is a $1$-cycle, then $\phi_*\psi(\gamma)=\operatorname{cls}\gamma$.

Proof.

Let $\gamma = \sum m_i\sigma_i$, where $\sigma_i$ are $1$-simplices.

Then we have $\partial\gamma=\sum m_i(\sigma_i(e_0)-\sigma(e_1))=0$; hence $\sum m_i(L_{\sigma_i(e_0)}-L_{\sigma_i(e_1)})$.

Therefore, by lemma 4.1-4.3, we have

Finally, we proved the Hurewicz theorem.

4.7 Theorem (Hurewicz).

If $X$ is a path-connected space with base point $x_0$, then

Proof.

From what we talked above, $\phi_*$ is the isomorphism. $\square$

4.8 Corollay.

• $H_1(S^1)=\mathbb Z$.
• If $X$ is simply connected, then $H_1(X)=0$.

4.9 Theorem.

Let $\phi^X:\pi_1(X,x_0)\to H_1(X)$​ be the Hurewicz map.

Then $\{\phi^X\}$ is a natural transformation from $\pi_1$ to $H_1$; that is the diagram

commutes, for each continuous map $h:(X,x_0)\to (Y,y_0)$.

Proof.

If $f$ be a loop in $X$ with base point $x_0$, then

$$

$$