久闻 Matlab 大名，但并没有学习过。在数学分析老师的要求下以及为了参加数学建模比赛开始学习 Matlab .

参考文献：Matlab Help Center

目录

• 安装&设置
• 数组和矩阵
• 输入输出
• 函数图像
• 逻辑和循环结构
• 未完待续

 

安装&设置

本人的 Matlab 安装包是从大学的软件库里面下载，并按照学校网站上的说明进行了激活。

如果你跟本人一样使用 Linux 系统并且是高分辨率屏幕，你可能会遇到 Matlab 分辨率的问题。这个问题在 ArchWiki 有解答。

打开 Matlab 后在命令行输入：

>> s = settings;s.matlab.desktop.DisplayScaleFactor
>> s.matlab.desktop.DisplayScaleFactor.PersonalValue = 1.5

然后重启 Matlab 即可。

另外不知为何 Matlab 显示中文字体会很奇怪，而英文字体又不能显示中文。遂在 Preferences > General 中将语言设置成英文，并在 Preferences > Fonts 中修改了字体。

另外 Matlab 的复制粘贴快捷键不是 Ctrl+C 与 Ctrl+V ，需要在 Preferences > Keyboard > Shortcuts 中更改。

 

数组和矩阵

Matlab 和 Python 有些类似，变量并不需要声明便可以直接赋值。

>> a = [1 2 3]

通过这种方式便获得了数组 a ，与其他编程语言不同的是，数组下标是从 1 开始而并不是从 0 开始，访问数组对应下标的元素使用的是 a(index) 而不是 a[index] .

因此我们在 Matlab 命令行中输入：

>> a(2)

得到的结果是：

ans =

     2

数组的赋值与其他语言类似：

>> a(2) = 10

一次性获得一个等差数列：

>> a = [1:10:101]

便能获得一个以 $1$ 为首项，以 $10$ 为公差，以 $101$ 为末项的等差数列（数组）。

当步长（公差）为 $1$ 的时候还可以省略中间的步长，写为：

>> a = [1:10]

这样即获得一个以 $1$ 为首项，以 $10$ 为末项，以 $1$ 为公差的等差数列。这种获得等差数列的方式还可以省略中括号，直接写成a = 1:10:101 或者 a = 1:10 .

在 Matlab 中，数组和矩阵是相同的概念，因此定义数组也是定义矩阵。刚刚我们知道如何定义只有一行的矩阵（一维数组），定义一般的矩阵（二维数组）也很简单（只需要在每一行的间隔处加个字符 ; ）：

>> A = [1 0 0; 0 5 0; 1 0 0.5]

这样我们便获得了一个 $3\times 3$ 的矩阵 $A$ .

Matlab 还可以轻松的将两个矩阵拼接到一块：

>> [A, A]
>> [A; A]

一些常见对矩阵的运算：

求 $\det A$：det(A)

求 $A^{-1}$ ：inv(A) 或 A^-1

求 $A^{T}$ ：A'

求 $A^k$ ：A^k

求 $AB$ ：A*B

求 $A+B$ ：A+B

求 $A-B$ ：A+B

将矩阵的全部元素求 $k$ 次方（不是矩阵的 $k$ 次方）：A.^k

将矩阵全体元素增加 $1$ ：A+1

将矩阵的全部元素放到某个一元函数里运算：sin(A) （以 $\sin x$ 为例，若将 $A$ 表示为 $(a_{ij})$，则运算结果是 $(\sin a_{ij} )$ ）

 

Matlab 还支持复数运算，其中虚数单位用 i 或 j 表示：

>> i^2
>> j^2

 

还可以调整 Matlab 数字浮点显示的位数（但只是修改显示的位数，并不改变浮点的运算精度）：

>> format short
>> 1.1

ans =

    1.1000

>> format long
>> 1.1

ans =

   1.100000000000000

 

输入输出

在 Matlab 中，我们可以像其他语言那样方便的进行字符串运算（在字符串内，单个双引号要写为 "" ）：

>> str = "The number is " + 10 + "."

字符串数组也与普通的数组类似：

>> A = ["a","bb","ccc"; "dddd","eeeeee","fffffff"]

同样我们可以像对矩阵进行某一函数运算一样对字符串数组进行某一函数运算：

>> strlength(A)

ans =

     1     2     3
     4     6     7

在 Matlab 中，字符串与字符数组是不同的概念：

>> a = 'abc';
>> a(1)

ans =

    'a'

字符数组的定义可以直接用 '<string>' 来定义。通过 string('<string>') 可以将字符数组转化为字符串，通过 char("<string>") 可以将字符串转化为字符数组。

输入（输入的格式与 Matlab 赋值变量的格式相同）：

>> x = input("Please input a number: ");

输入一个字符数组：

>> x = input("Please input a string: ",'s');

输出：

>> disp("Hello, world!");

 

函数图像

一元函数图像：

在 Matlab 中新建 Script ，在里面输入：

x = linspace(-10, 10, 51); % 在区间[-10,10]中均匀选择51个点构成数组，包括-10和10
y = x.^2;
plot(x,y); % 画图

然后我们就得到了 $y=x^2$ 的函数图像：

我们还可以给座标轴添加名称，以及添加图像标题：

x = linspace(-10, 10, 51);
y = x.^2;
plot(x, y);
xlabel("x");
ylabel("x^2");
title("Plot of the parabola");

设置曲线的形状及颜色：

x = linspace(-10, 10, 51);
y = x.^2;
plot(x, y, "r--");

在字符串 r-- 中 r 代表颜色为红色，-- 代表样式，除此之外还有 * o : 等样式。

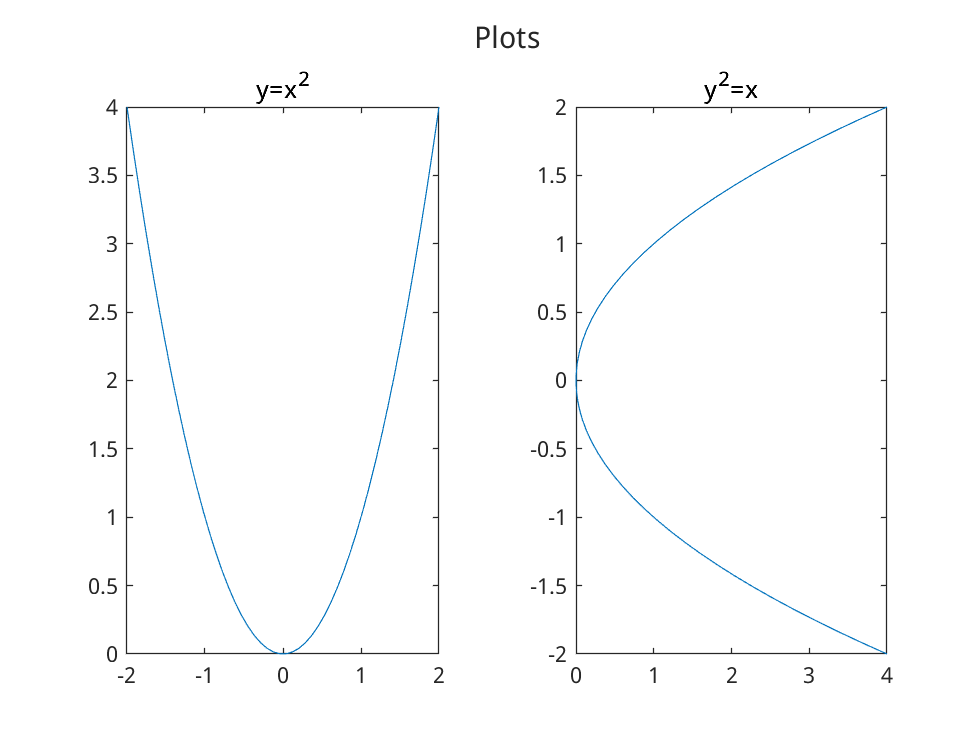
绘制第二条曲线：

x = linspace(-2, 2, 50);
y = x.^2;
plot(x, y, "r--");
hold on; % 在同一个图像中画图需要使用hold on
plot(y, x, "b");
legend("y=x^2","y^2=x"); % 标记两条曲线的名称
hold off; % 结束画图

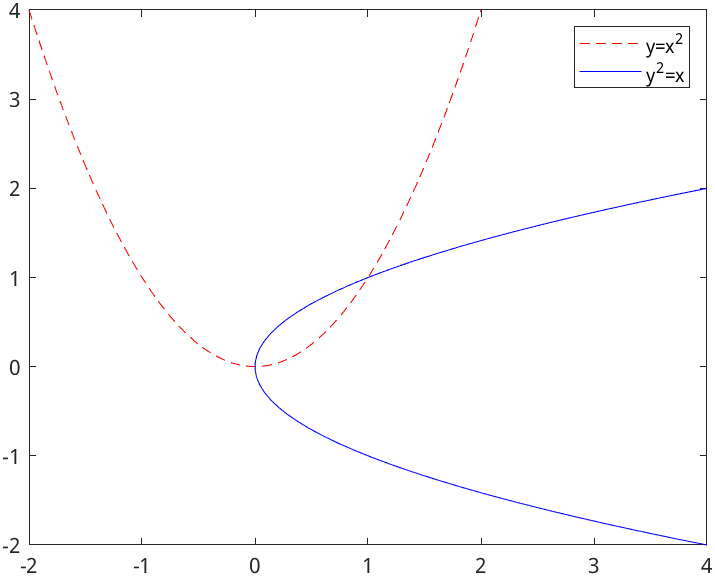
同时绘制多个图像：

t = tiledlayout(1,2); % 布局，1行2列
title(t,"Plots"); % 最上方的大标题

nexttile;
x = linspace(-2, 2, 50);
y = x.^2;
plot(x, y);
title("y=x^2");

nexttile;
plot(y, x);
title("y^2=x");

二元函数图像：

一直以来对马鞍面（双曲抛物面）这个神奇的曲面感兴趣，于是就来绘制一下马鞍面。

马鞍面的一般方程为 $\frac {x^2}{a^2}-\frac{y^2}{b^2}=2pz$ 转化一下就是 $z= \frac {x^2}{2pa^2}-\frac{y^2}{2pb^2}$ ，然后令 $f(x,y)= \frac {x^2}{2pa^2}-\frac{y^2}{2pb^2}$ ，即可转化为普通的二元函数。

我们挑选一个简单的马鞍面方程： $f(x,y)=\frac {x^2}{25}-\frac{y^2}{16}$ .

x = linspace(-5,5,20);
y = x'; % y 座标的矩阵（只有一列的矩阵）为 x 座标矩阵的转置
z = x.^2/25-y.^2/16;
surf(x,y,z); % 三维绘图

 

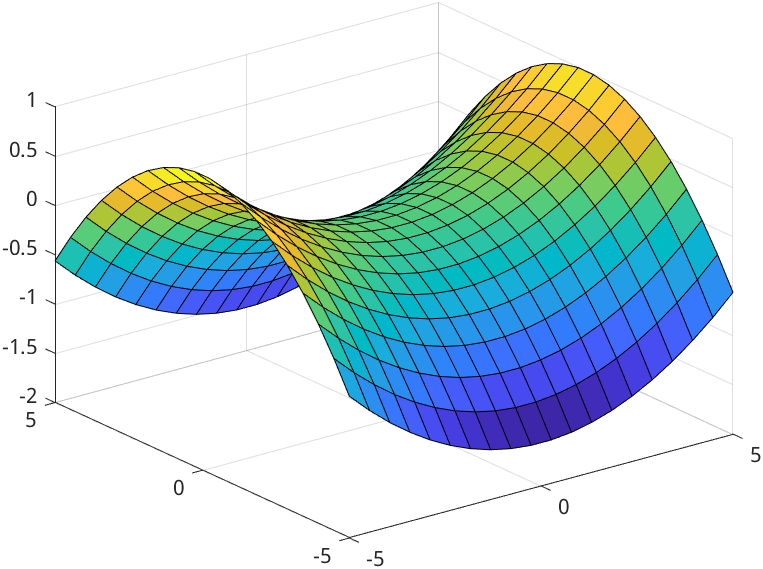
这块我们可以注意到有一个奇怪的运算 x.^2/25-y.^2/16 .

我们知道 x.^2/25 为一个只有一行的矩阵，y.^2/16 为一个只有一列的矩阵，它们之间怎么能进行减法运算呢？

事实上 Matlab 会这样处理： $z_{ij}=\frac{x_{1i}^2}{25}-\frac{y_{j1}^2}{16}$ .（这里的 $z_{ij}$ 表示 $z$ 矩阵的第 $i$ 行第 $j$ 列）

 

逻辑和循环结构

循环结构有些类似很多语言中的 foreach 语法：

N = 100;
f(1) = 1;
f(2) = 1;

for n = 3:N % 按顺序将 n 赋值为数组 3:N 中的每一个元素并执行后面的语句
    f(n) = f(n-1) + f(n-2);
end
f(1:10)

逻辑结构：

num = randi(100); % 生成一个 [1,100] 内的整数随机数
if num < 34
   sz = 'low';
elseif num < 67
   sz = 'medium';
else
   sz = 'high';
end
disp(num + " is " + sz);