难度&推荐指数:
- 思维难度:提高+/省选-
- 实现难度:普及/提高-
- 推荐指数:8.5(推荐指数最高为10.0)
题目翻译
Figure Fixing
数值修正
You have a connected undirected graph made of $n$ nodes and $m$ edges. The $i$-th node has a value $v_i$ and a target value $t_i$.
你有一个连通无向图,它有 $ n $ 个节点和 $ m $ 条边。第 $ i $ 个节点有权值 $ v_i $ 和目标权值 $ t_i $ .
In an operation, you can choose an edge $(i,j)$ and add $k$ to both $v_i$ and $v_j$, where $k$ can be any integer. In particular, $k$ can be negative.
在一次操作中,你可以选定一条边 $ (i,j) $ 和一个整数 $ k $ ,然后将 $ v_i $ 和 $ v_j $ 同时增加 $ k $ . $ k $ 可以是任意整数,特别的,$ k $ 可以是负数。
Your task to determine if it is possible that by doing some finite number of operations (possibly zero), you can achieve for every node $ i $, $ v_i=t_i $.
你的任务是确定是否可能用有限次操作使得所有的节点的权值都变为目标权值,操作次数可以为 $ 0 $ .
题解
算法:二分图染色
首先我们可以将每个节点的权值都当成 $ v_i-t_i $ ,然后题目就转化为了将每个节点的权值都变为 $ 0 $ .
可以注意到,我们的一次操作会让所有的节点权值和增加 $ 2k $ ,而 $ 2k $ 一定是一个偶数。也就是说如果所有节点的初始权值和为奇数,那么这种情况必然无解。接下来我们再来考虑,所有节点的初始权值和为偶数的情况。
我们随意选择图中的任意一条链。
如果这条链的长度为奇数,那么我们可以用如图所示的方式让链的两端同时增加 $ k $ .
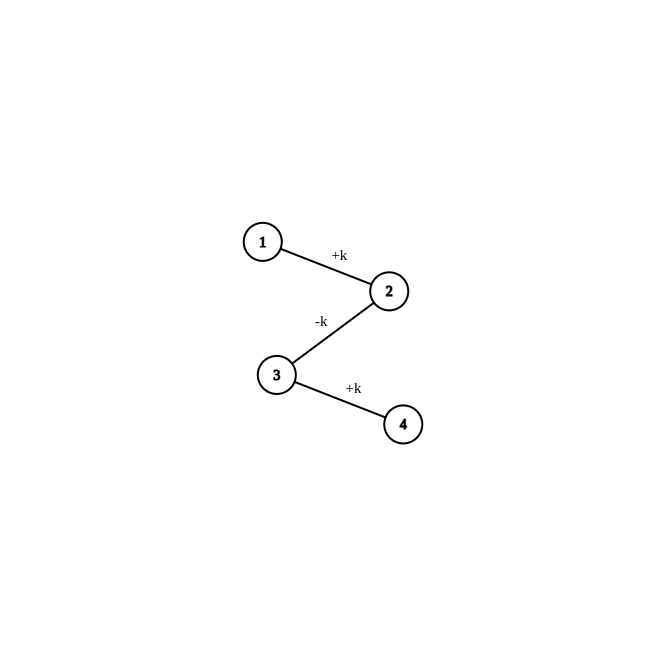
如果这条链的长度为偶数,那么我们可以用如图所示的方式让链的一端增加 $ k $ ,另一端减少 $ k $ .
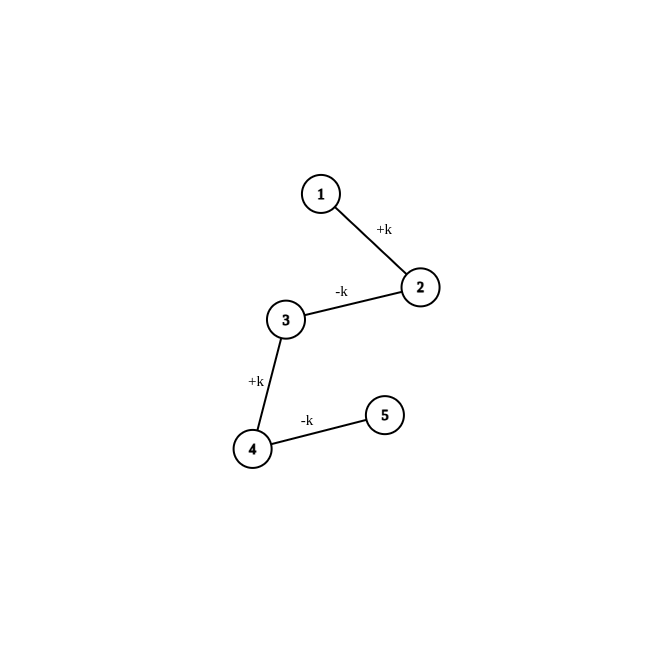
那么也就是说,我们可以利用这两个性质,将当前节点的权值“传递”到其他的节点。
接下来我们再考虑一下环的情况。我们不妨设环上的点是 $ 1,2,…,n $ ,当 $ n $ 为奇数时,可以将环“拆”为两部分,一部分是仅有两个节点的链 $ 1,2 $ ,另一部分是 $ 2,3,…,n,1 $ 这条链。
可以注意到在第一条链中 $ 1,2 $ 可以同时增加 $ k $ ,而在另一条链中,$ 1,2 $ 可以一个增加 $ k $ 另一个减少 $ k $ 。也就是说,我们可以先让它俩同时加 $ k $ 再让 $ 1 $ 增加 $ 2 $ 减少 $ k $ 就能实现 $ 1 $ 这个节点的自增(可以自增任意一个偶数)。所以,任意一个奇环上的点都可以自增任意一个偶数。
当 $ n $ 为偶数时,环并没有我们可以利用的特殊性质。
由于图里面的所有节点的权值和是偶数,那么权值为奇数的节点一定有偶数个。我们将权值为奇数的点两两凑一对,用上述的“传递”的方式将它们的权值都变成偶数。
如果一个图里面存在奇环,那么我们可以将图中全部节点的权值都传递到其中一个奇环上,接着用奇环上的点可以自增的性质全部清零。也就是说如果一个图存在奇数环并且它的权值和为偶数,那么它一定是有解的。
我们知道一个图是二分图当且仅当它没有奇环,我们已经考虑了不是二分图的情况,接下来我们再考虑一下二分图的情况。
我们把二分图划分为 $ S_1 $ 和 $ S_2 $ 两个集合。由于图是连通的,那么对于任意 $ x \in S_1,y\in S_2 $,总存在一条从 $ x $ 到 $ y $ 的路径,再结合二分图的性质,这条路径的长度一定是奇数。那么如果 $ S_1 $ 内节点的权值和与 $ S_2 $ 内节点的权值和相等,我们通过上文的权值“传递”一定可以将图的全部节点权值清零,如果不相等,无论我们怎么“传递”,都不可能让全部节点权值清零。
到这里,这道题的做法就很明了了。
#include<stdio.h>
#define MAXN 200005
#define MAXM 200005
typedef long long ll;
struct node{
int eh;
int v;
int c;
}V[MAXN];
ll s[2];
struct edge{
int next;
int to;
}E[MAXM*2];
int tot;
void add_edge(int from,int to)
{
E[++tot]=(edge){V[from].eh,to};
V[from].eh=tot;
}
bool vis[MAXN],flag;
void dfs(int i,int c)
{
if(vis[i]&&V[i].c!=c)
{
flag=true;
return;
}
if(vis[i]) return;
V[i].c=c;
vis[i]=true;
s[c]+=V[i].v;
for(int p=V[i].eh;p;p=E[p].next)
{
dfs(E[p].to,c^1);
if(flag) return;
}
}
int main()
{
int i,T,n,m,t,x,y;
ll sum;
scanf("%d",&T);
while(T--)
{
sum=0;
tot=0;
s[0]=s[1]=0;
flag=false;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
scanf("%d",&V[i].v);
for(i=1;i<=n;i++)
{
scanf("%d",&t);
V[i].eh=0;
V[i].v-=t;
sum+=V[i].v;
vis[i]=false;
}
for(i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
add_edge(x,y);
add_edge(y,x);
}
if(sum%2!=0)
{
printf("NO\n");
continue;
}
dfs(1,0);
if(flag||s[0]==s[1]) printf("YES\n");
else printf("NO\n");
}
return 0;
}